Bu yazının devamında 3 veya daha fazla sayıda grubu, bir değişken bakımından karşılaştırmak için kullanılan tek faktörlü varyans analizi (One-way Anova) anlatılmıştır. Yazının sonunda, analizin SPSS ile nasıl yapılacağı, resimlerle anlatılarak örnek bir analiz sonucu yorumlanmıştır. Yazıyı etkin şekilde okuyabilmek için istatistik.gen.tr size firefox kullanmanızı önerir. Resimlerin daha büyük ve net halleri için lütfen mouse imlecini resimlerin üzerinde bekletin.
Tek faktörlü Varyans analizi (ANalyis Of VAriance) 3 ya da daha çok grup arasında, belirli bir değişkene dayalı olarak farklılık olup olmadığını belirlemek amacıyla kullanılır. Örneğin “alt, orta ve üst sosyo-ekonomik düzeylerdeki kişilerin depresyon düzeyleri birbirinden farklı mıdır?” sorusuna, bu gruplardan toplanmış olan depresyon puanlarını karşılaştırarak varyans analizi cevap verebilir. Ya da yönetici, işçi, memur ve işsizlerin yaşam doyumu düzeylerinin birbirinden farklı olup olmadığı yine tek faktörlü varyans analizi ile test edilebilir. Tek faktörlü varyans analizinden deneysel çalışmalarda da yararlanılabilir. Deney, kontrol (plasebo) ve bekleme gruplarının, deneysel işlem sonrası son test puanlarının farklı olup olmadığı tek faktörlü varyans analizi ile test edilebilir.
|
Varyans analizi, Sir Ronald Aylmer Fischer (portresi yandadır) tarafından bulunmuş olan bir dağılımı kullanmaktadır. Temelde Fischer’in dağılımı, beklenen ve gözlenen değerlerin uyumunu test etmeye yarayan chi-square (kay-[ya da yanlış fakat yaygın bir okuyuş olarak ki] kare okunur) dağılımından türetilmiş bir dağılımdır. Temel olarak varyans analizi, gruplar arasındaki değişkenliği (farklılaşmayı-varyansı), grupların içindeki bireyler arasındaki değişkenliğe (farklılaşmaya-varyansa) oranlar. Analizin amacı, gruplar arasındaki farklılaşmanın, bireyler arasındaki farklılaşmadan büyük olup olmadığını tespit etmektir. Bir örnekle açıklamak gerekirse: |
 |
Araştırmacı, üç farklı sosyoekonomik düzeyden kişilerin yaşam doyumu düzeylerini karşılaştırmak istemektedir. Eğer gruplar arasında fark varsa, her bir sosyoekonomik düzey grubu kendi içinde, yaşam doyumu bakımından küçük bir varyansa sahip olmalı yani yaşam doyumu puanları bakımından çok homojen olmalı fakat yine yaşam doyumu bakımından gruplardaki her bir birey bir diğer gruptaki herhangi bir bireyden hatırı sayılır ölçüde farklı olmaldır. Aşağıdaki şekil bunu göstermektedir.
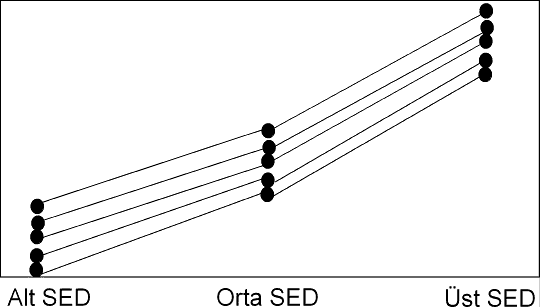
Bazı durumlarda farklı gruplarda yer alan bireyler arasındaki farklılıktan (gruplararası varyanstan) çok aynı grupta yer alan bireyler arasındaki farklılık (grupiçi varyans) daha büyük olabilir. yani yukarıdaki terimlerle söylenecek olursa grup içi varyans, gruplararası varyanstan daha büyük olabilir. Aşağıda bu durum gösterilmiştir:
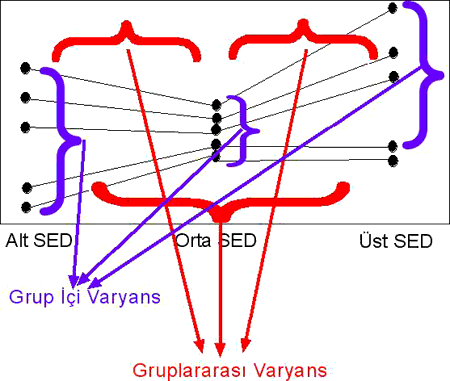
Yukarıdaki gibi bir durumda alt-orta ve üst sosyoekonomik düzeyden kişilerin yaşam doyumlarının birbirinden farklı olmadığı bir durum sözkonusudur. Dikkat edilecek olursa alt ve orta sosyoekonomik düzeyden bireylerin büyük çoğunluğunun yaşam doyumları birbirine eşit gübü görünmektedir. Orta sosyoekonomik düzeyden bireyler ise hem alt hem de üst sosyoekonomik düzeyden bireylerin yaşam doyumlarıyla hemen hemen aynı düzeydedir. Dolayısı ile gruların farklılığından çok, aynı grupta yer almasına rağmen birbirinden çok farklı yaşam doyumuna sahip bireyler sözkonusudur.
İşte varyans analizinin yapmaya çalıştığı şey budur. Gruplararasındaki varyansı ve grupların kendi içlerindeki varyansı hesaplayarak birbirine oranlamak ve bu varyansların büyüklüklerine göre bir karar vermektir.
Gruplararası varyansı bulabilmek için, öncelikle grupların herbirinin, bütün grupların birleşiminden oluşan ve hepsini temsil eden genel ortalamadan ne kadar farklılaştığını bulmak gerekir. Burada amaç şudur:
t testi yapılırken iki grubun birbirinden farklı olduğunu bulabilmek için bu iki grubun ortalamalarının birbirinden farklarını bulup ortalamaların standart hatalarına bölmek yetiyordu. Fakat varyans analizinde genelde ikiden çok grup birbiriyle karşılaştırılır. Her bir grup ikişerli olarak karşılaştırılırsa sonuçta “işte bu gruplar arasında fark vardır” kararını %5 hata payıyla değil, her bir karşılaştırmada ayrıca yaptığımız %5’lik (ya da daha az) hataların toplamı kadar hata ile söyleyebiliriz. Oysa ki istatistik kullanılarak bir karar verilecekse, bu kararın önceden belirlenmiş sabit bir hata düzeyinde verilmesi gerekir. Bilindiği gibi bu hata düzeyi özellikle sosyal bilimlerde %5 veya %1 olarak alınır.
İşte bu hatanın her bir çift karşılaştırmasında artmasını engellemek için varyans analizi, karşılaştırılacak grupların hepsini büyük ve tek bir grup gibi düşünür ve bu büyük grup içindeki grupların tek tek bu büyük gruptan ne kadar farklı olduklarını bulmaya çalışır.
şekil üzerinden konuşacak olursak kırmızı parantezle gösterilen farklılaşmaların toplamının, mavi parantezle gösterilen farklılaşmaların toplamından daha fazla olması gerekir.
Peki, gruplararası ve grupiçi varyansı nasıl hesaplayacağız. Gruplararası varyansı tıpkı yukarıda söylediğimiz gibi her bir grubun ortalamasını, bütün grupların biraraya gelerek oluşturduğu genel ortalamadan çıkaracağız ve sonra bunları toplayacağız. Grup içi varyansı ise her bir grubun içindeki bireylerin o grubun ortalamasından ne kadar farklılaştıklarını bularak hesaplayacağız. Yani her bir grup için ayrı ayrı, bireylerin puanlarını grup ortalamasından çıkarıp bunları toplayacağız. Son olarak da bu kareler toplamlarının bize varyansı verebilmesi için her birini kendi serbestlik derecesine böleceğiz. Birazdan “serbestlik derecesi” nin ne olduğunu göreceğiz.
Fakat bazen grup ortalamasından büyük olanlar olacak bazen de küçük olanlar olacaktır. Bu puanlar toplanınca ortalamadan büyükler ve küçükler birbirini götürüp sonuçta sıfır gibi bir değer bulmak mümkün olabileceğinden ve bu durum da işleri karıştırabileceğinden ortalamadan olan farkların kareleri alınacaktır. Böylece sıfır’ın yaratabileceği problemden kurtulunacaktır.
Serbestlik derecesine bölünmeden önce grup içi ve gruplararası farklılaşmanın bütününü bize veren değerlere kareler toplamı denir. Biraz önce, sonucun sıfır çıkması ihtimalinden kurtulmak için grup içindeki ve gruplararasındaki ortalamadan farklılaşmaların karelerinin alındığı söylenmişti. Bu nedenler kareler toplamı denmektedir.
Gruplararası varyans hesaplanmadan önce gruplararası kareler toplamı ve grupiçi kareler toplamı hesaplanmalıdır. Daha sonra bunlar kendi serbestlik derecelerine bölünerek kolayca varyansa çevrilebilir.
Gruplararası kareler toplamının hesaplanması:
Her bir grubun ortalamasının genel ortalamadan çıkarılması ve elde edilen değerlerin karesinin alınması, sonra da bu değerlerin toplanarak serbestlik derecesine bölünmesi.
Matematik simgelerle yazarsak
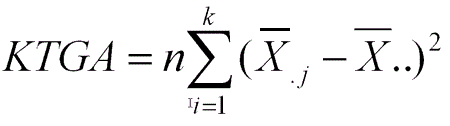
KTGA= Gruplararası Kareler Toplamı
Tekrar okuyacak olursak 1. gruptan k. (k’ıncı) gruba kadar, her grubun ortalaması genel ortalamadan çıkarılacak ve elde edilen değerin karesi alınacak. Sonra da bu değerler toplanacak.
Aynı basitlik grupiçi varyans için de geçerlidir.
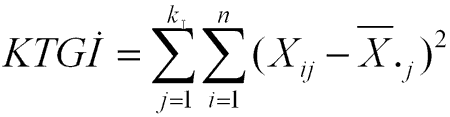
KTGİ= Gruplariçi Kareler Toplamı
Tekrar okunacak olursa, her bir grup ve gruplardaki tüm bireyler için, bu bireylerin puanlarından bu bireylerin dahil oldukları grubun ortalamasını çıkar ve karesini al. Sonra da tüm bu değerleri topla.
Bir örnek üzerinde tekrarlanacak olursa durumun basitliği şöyle gösterilebilir:
Formüllere uygun yerleştirmeyi yaptığımızda:
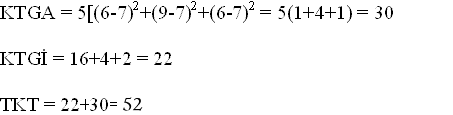
Olarak buluruz.
TKT olarak görülen grupiçinin ve gruplararası kareler toplamlarının toplanmasıyla elde edilir.
Bu noktadan itibaren gruplararası ve grup içi varyansın hesaplanması mümkündür. Bunun için gruplararası ve grupiçi kareler toplamları kendi serbestlik derecelerine bölüncektir.
Serbestlik derecesi:
Yukarıda hesapladığımız gruplararası ve grupiçi kareler toplamları “ortalamadan farklılıkları gösteren” değerler olarak düşünüldüğünde, birer hata katsayısı gibi değerlendirilebilirler. Her hatayı oluşturan bileşenler vardır. örneğin gruplararası kareler toplamı değerinin oluşmasına kaç grup varsa onların hepsi katılır. Grupiçi kareler toplamı değerinin oluşmasına gruplardaki bireylerin hepsi katkıda bulunur. İşte bu hata katsayılarının, kendilerinin oluşumuna katkıda bulunan herkese/her gruba paylaştırılması sırasında hata paylarını kime önce atayacağımız konusunda serbestizdir. Örneğin gruplararası kareler toplamını gruplara pay etmek için her bir gruba atama yaptıkça sona doğru elimizde kalan hata miktarını son gruba vermek zorundayızdır. Dolayısıyla son grup hariç diğer gruplarda hatanın kime dağıtılacağı konsunda serbest olabiliriz. Dolayısıyla gruplar söz konusu olduğunda serbestlik derecemiz grup sayısının bir eksiğidir. Grup içi varyansta ise bireylere bu kareler toplamları pay edilirken ilk bireylerde kimi seçeceğimiz konusunda serbestizdir. Fakat örneğin birinci grubun sonuna geldiğimizde o son kişiye o grup için elimizde kalan son parçacığı atamak zorundayızdır. Dolayısı ile her grupta bu sonuncu kişide serbest olamayacağımız için gruplar içi varyans sözkonusu olduğunda serbestlik derecesi toplam kişi sayısından grup sayısının çıkarılması ile bulunur. Bunu tersten düşünürseniz elde ettiğimiz kareler toplamını yeniden üretmek için tamamen rastgele sayıları gruplara atarak ilerlesek en son grubun değerini rastgele atamayacak durumda oluruz. Çünkü elimizde önceden bildiğimiz bir kareler toplamı vardır ve bu değeri elde edebilmek için sonuncu grubun değerini rastgele değil tam da elimizdeki önsel değeri verecek şekilde belirlemek “zorundayızdır”. Serbestlik derecesi olmadan istatistiksel testlere ait dağılımların şeklini belirlemek imkansızdır.
Varyans analizini spss programında yapabilmek için şu aşamalar izlenir.
Önce gruplama değişkenleri ve daha sonra maddeler spss programına girilir.
bu işlem bittiğinde aşağıdaki gibi bir görüntü oluşur.
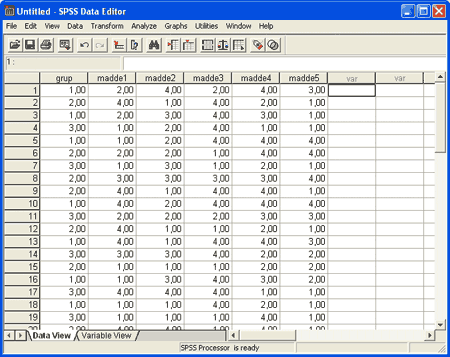
Daha sonra analiz, maddelerin toplam puanlarından yapılacağı için maddelerin toplatılması, ölçeğin toplam puanının bulunması gerekmektedir. bunun için sırasıyla aşağıdaki işlemler yapılır.
Önce transform menüsünden compute kısmına girilir.
,
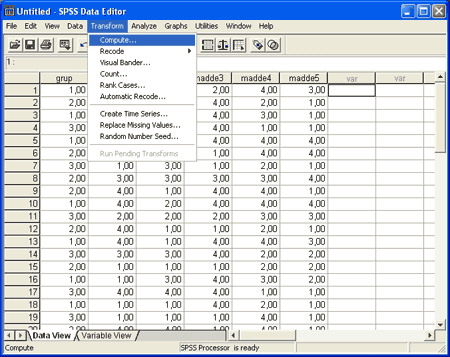Compute’a tıklandığında aşağıdaki gibi bir pencere açılır.
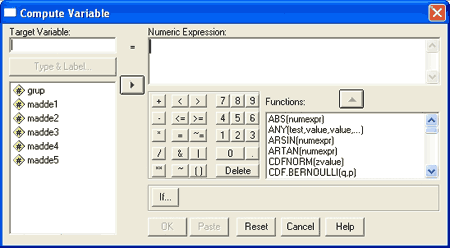
buradan target variable kısmına oluşturulacak toplam puan değişkeninin adı yazılır. Burada toplam adı verilmiştir görüleceği gibi.
numeric expression kısmına ise nelerin toplanacağı atılır.
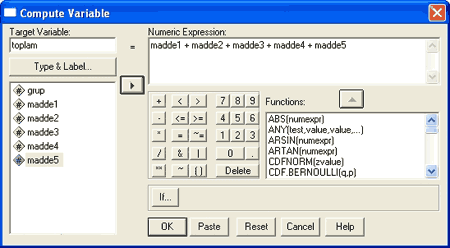
işlem bitip OK’e tıklandığında ise o maddelerin toplamı veri dosyasına yazılır ve şöyle bir durum oluşur:
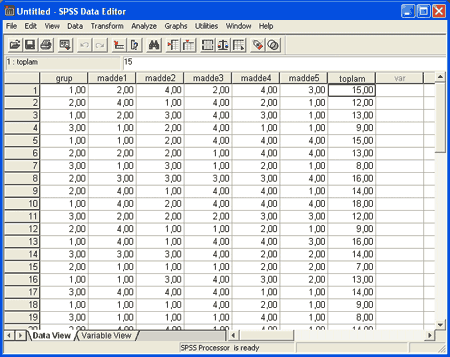
Böylece artık varyans analizine geçilebilir. Varyans analizi yapabilmek için aşağıdaki resimde gösterilen menüye girmek gerekir.
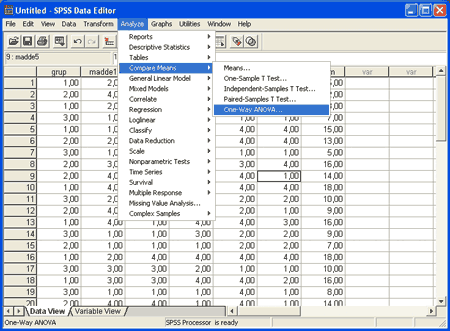
One-Way anova tıklandığında şöyle bir pencere açılır.
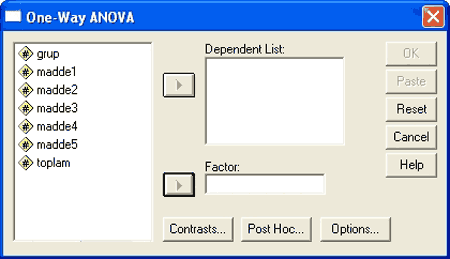
Factor kısmına gruplamayı gösteren değişkeni, dependent list kısmına ise gruplar arasında ne bakımından fark aranıyorsa o değişeni atmak gerekir. burada toplam puan bakımından fark aranmaktadır. Bu nedenle değişkenler aşağıdaki şekildeki gibi yerleştirilmelidir.
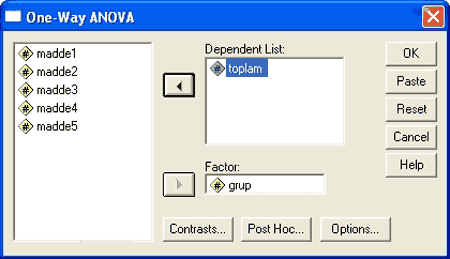
Daha sonra burada sağ alt köşede görülen Options kısmına girilerek aşağıdaki işaretlemeler yapılmalıdır.
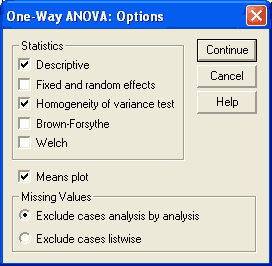
Daha sonra Continue ile devam edilir ve aşağıdaki pencereye geri dönülür.
Burada OK tıklanırsa aşağıdaki analiz sonucu ile karşılaşılır
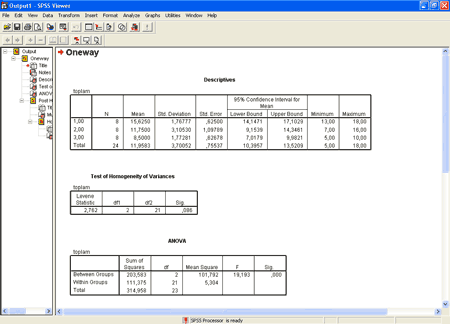
burada test of homogenity of variances tablosunda (2. tablo) sig. (anlamlılık) değeri 0,05’ten küçük çıktı ise varyanslar homojen değil demektir ve varyans analizi için oldukça büyük önem taşıyan bir varsayımın karşılanamadığı anlamına gelir. bu durumda varyans analizine devam etmemek gerekir. Fakat bu örnekte olduğu gibi test of homogenity of variances tablosundaki değer 0,05’ten büyük çıktı ise varyansların homojen olduğu kabul edilir ve varyans analizi tablosu olan ANOVA tablosu okunmaya devam edilir.
Asıl varyans analizi tablosu 3. tablo olan ANOVA tablosudur. ANOVA tablosunda en sonraki sig. değeri 0,05Ten küçükse karşılaştırılan grupların ortalamaları arasında anlamlı bir fark olduğuna karar verilir. bu örnekte de üstteki resimde görüleceği gibi gruplar arasında anlamlı bir farklılık olduğu görülmektedir. Varyans analizi karşılaştırılan grupların hangileri arasında fark olduğunu bildiremez. Bu nedenle anlamlı fark bulunduğu zaman bu farkın hangi gruplar arasındaki farktan kaynaklandığını bulmak amacıyla post-hoc test denen karşılaştırmaların yapılması gereklidir. Eğer ANOVA sonucunda sig. değeri 0,05’ten büyük çıktı ise post-hoc test yapılmaz post-hoc test yapabilmek için yine üstte anlatılan varyans analizi aşamaları takip edilir. şu aşamaya gelindiğinde
Altta ortada bulunan Post Hoc düğmesine tıklanır. Buna tıklandığında şöyle bir pencere açılır.
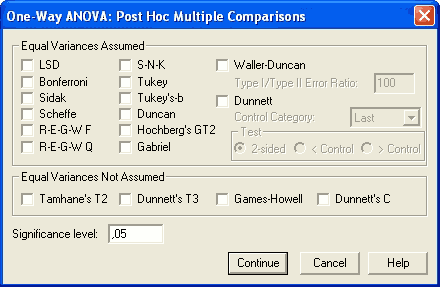
Buradan araştırmanın desenine uygun bir post hoc test seçilir. (daha sonra ayrıntılarıyla açıklanacaktır)
Çoğunlukla Tukey testi uygun bir post hoc karşılaştırma testi olarak düşünülür. Örnek olarak burada Tukey post-hoc testi seçilmiştir.
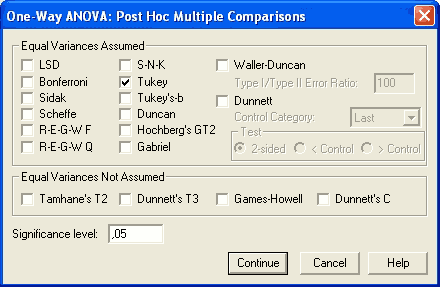
buradan continue tıklanarak devam edilir. tekrar varyans analizi ekranına gelinmiş olur.
yine OK tıklanarak devam edilirse bu sefer varyans analizi post-hoc testle birlikte yapılır.
ve karşımıza şöyle bir analiz sonucu gelir.
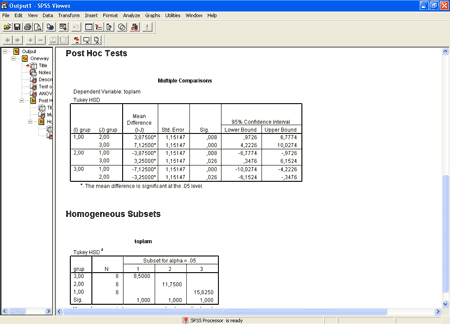
Yukarıdaki POST HOC TESTS tablosunu görebilmek için çıktı sayfasını biraz aşağı almanız gerekebilir.
Bu tabloda dikkat edilecek olursa solda I (grup) – J (grup) şeklinde gösterilen gruplar birbiriyle karşılaştırılacak olan gruplardır. Burada spss tüm grupları birbirleriyle karşılaştırmış ve anlamlı fark olup olmadığını test etmiştir. Önce 1. grup ile 2. grubu karşılaştırmış Sonra 1. grup ile 3. grubu karşılaştırmıştır. 1. grup ile 2. grubu karşılaştırmış ve bu grupların ortalamaları arasında 3,87500 puan kadar fark bulmuştur. bu gruplar için yapılan karşılaştırma sonucunda sig değeri 0,008 bulunmuştur. Bu değer 0,05’ten küçük olduğu için 1. grup ile 2. grubun ortalamaları arasında anlamlı bir farklılık olduğuna karar verilebilir. 1. grubun ve 2. grubun ortalamalarına bu çıktı dosyasının en üstündeki descriptives tablosundan bakılacak olursa
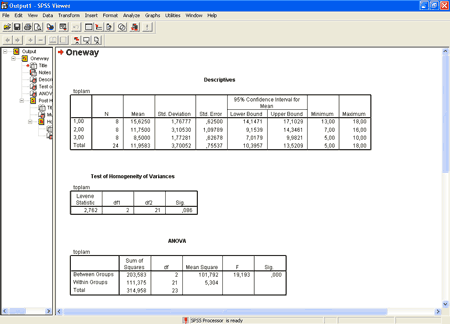
1. grubun ortalamasının (mean) 15,6250 ve 2. grubun ortalamasının da 11,7500 olduğu görülür. Yani 1. grubun ortalaması 2. grubun ortalamasından istatistiksel olarak daha büyüktür. Eğer post-hoc tablosunda 1. grup ile 2. grup arasında fark çıkmamış olsaydı, yani post hoc tabloasundaki sig. değeri 0,05’ten büyük çıkmış olsaydı. 1. grubun ortalaması 2. grubun ortalamasından daha büyük olduğu halde iki grubun ortalamasını birbirine eşit sayacak ve “aslında farklı gibi görünüyor ama aralarında fark yoktur” kararı verecektik.
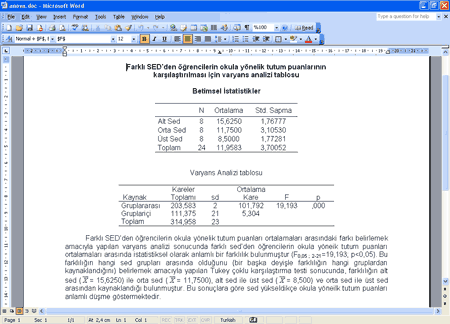
Daha sonra yapılan bu işlemler rapor haline dönüştürülür ve şu şekilde görünmesi sağlanır.
Soru ve önerilerinizi aşağıdaki yorum bölümüne yazabilirsiniz
Bir yanıt yazın